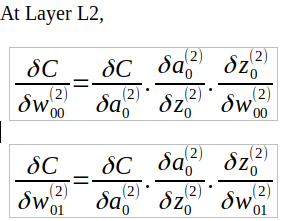Deep Learning with R
Neural network fundamentals
Mikhail Dozmorov
Virginia Commonwealth University
2020-06-08
Deep Learning Prerequisites
For each machine- and deep learning algorithms, we need:
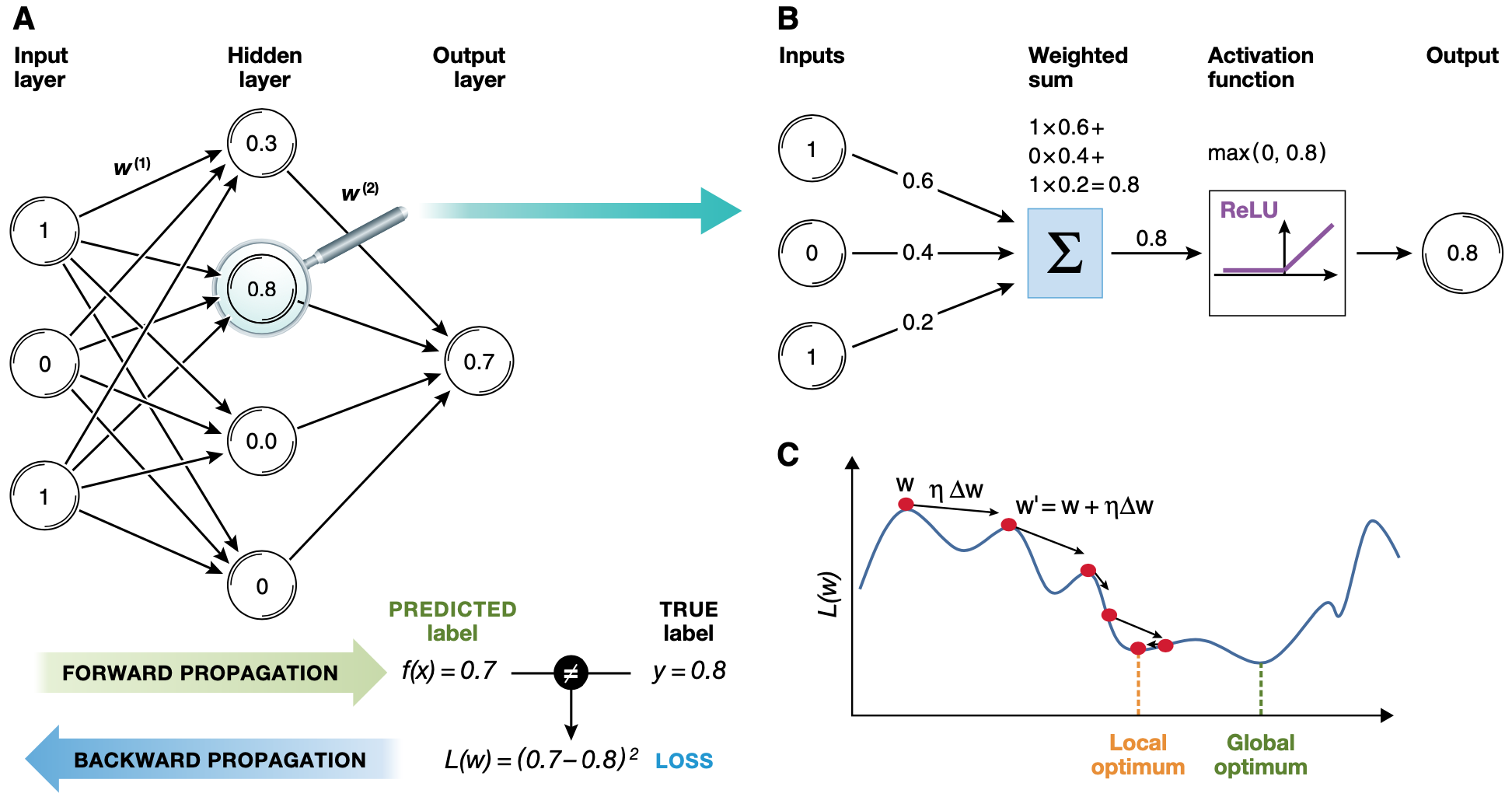
Input data - samples and their properties. E.g., images represented by color pixels. Proper data representation is crucial
Examples of the expected output - expected sample annotations
Performance evaluation metrics - how well the algorithm's output matches the expected output. Used as a feedback signal to adjust the algorithm - the process of learning
How deep learning learns
Creates layer-by-layer increasingly complex representations of the input data maximizing learning accuracy
Intermediate representations learned jointly, with the properties of each layer being updated depending on the following and the previous layers
The beginning of Deep Learning
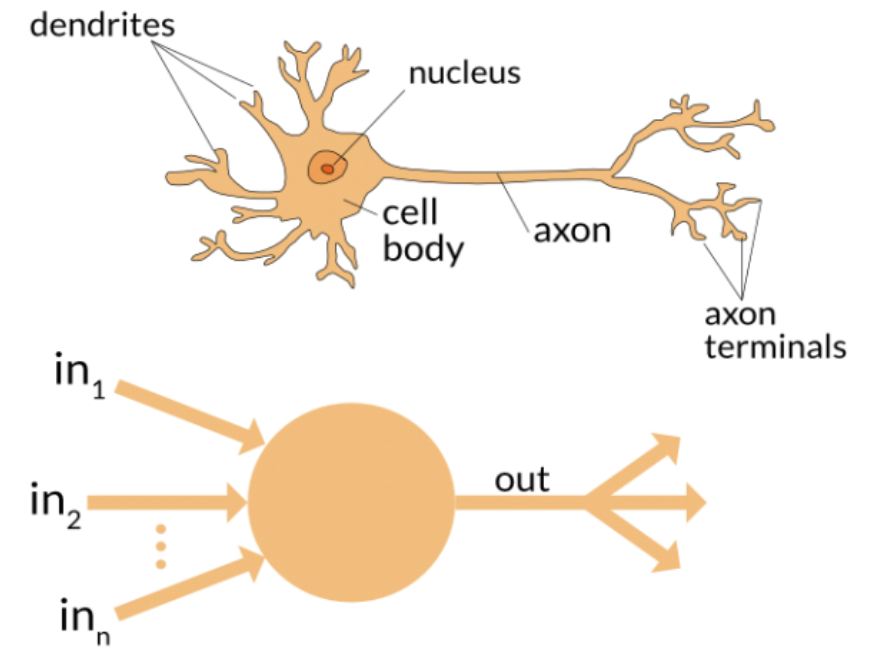
- A generic Deep Learning architecture is made up of a combination of several layers of "neurons"
- The concept of a "neuron" was proposed in the 1950s with the well-known Rosenblatt "perceptron", inspired by brain function
- The multilayer perceptron (MLP) is a fully-connected feedforward neural network containing at least one hidden layer
White, B.W.; Rosenblatt, F. Principles of Neurodynamics: Perceptrons and the Theory of Brain Mechanisms. Am. J. Psychol. 1963
Deep Learning winter and revival
Widespread belief that gradient descent would be unable to escape poor local minima during optimization, preventing neural networks from converging to a global acceptable solution
During 1980s, 1990s, deep neural networks were largely abandoned
In 2006, deep belief networks revived interest to deep learning
In 2012, Krizhevsky et al. presented a convolutional neural network that significantly improved image recognition accuracy
GPU technologies enabled further development
Hinton GE, Osindero S, Teh Y-W. A fast learning algorithm for deep belief nets. Neural Comput. 2006
The Perceptron: Linear input-output relationships
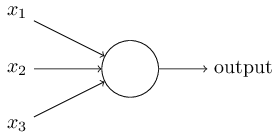
- Input: Take x1=0, x2=1, x3=1 and setting a threshold=0
- If x1+x2+x3>0, the output is 1 otherwise 0
- Output: calculated as 1
The Perceptron: Adding weights to inputs
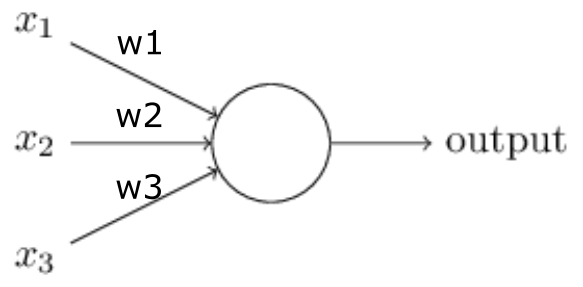
^y=g(∑mi=1xiwi)
- ^y - the output
- ∑ - the linear combination of inputs
- g - a non-linear activation function
- Weights give importance to an input. For example, you assign w1=2, w2=3 and w3=4 to x1, x2 and x3 respectively. These weights assign more importance to x3.
- To compute the output, we will multiply input with respective weights and compare with threshold value as w1∗x1+w2∗x2+w3∗x3>threshold
https://www.analyticsvidhya.com/blog/2017/05/neural-network-from-scratch-in-python-and-r/
The Perceptron: Adding bias
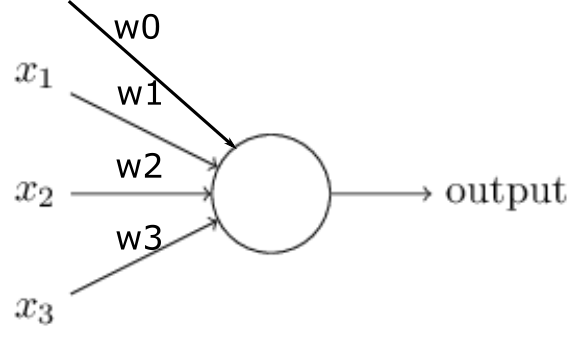
^y=g(w0+∑mi=1xiwi)
- w0 - bias term
^y=g(w0+XTW)
- Bias adds flexibility to the perceptron by globally shifting the calculations and allowing the weights to be more precise
- Think about a linear function y=ax+b, where b is the bias. Without bias, the line will always go through the origin (0,0) and we get poorer fit
- Input consists of multiple values xi and multiple weights wi, but only one bias is added. For i=3, the linear representation of input will look like w1∗x1+w2∗x2+w3∗x3+1∗b
https://www.analyticsvidhya.com/blog/2017/05/neural-network-from-scratch-in-python-and-r/
Multi-layer neural network
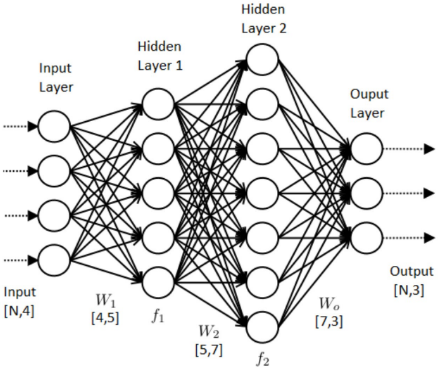
- Input - a layer with n neurons each taking input measures
- Processing information - each neuron maps input to output via nonlinear transformations that include input data xi, weights wi, and biases b
- Output - Predicted probability of a characteristic associated with a given input
https://www.datasciencecentral.com/profiles/blogs/how-to-configure-the-number-of-layers-and-nodes-in-a-neural
Layers
Deep learning models are formed by multiple layers
The multi-layer perceptron (MLP) with more than 2 hidden layers is already a Deep Model
Most frequently used layers
- Convolution Layer
- Max/Average Pooling Layer
- Dropout Layer
- Batch Normalization Layer
- Fully Connected (Affine) Layer
- Relu, Tanh, Sigmoid Layer (Non-Linearity Layers)
- Softmax, Cross-Entropy, SVM, Euclidean (Loss Layers)
Fitting the parameters using the training set
Parameters of the neural network (weights and biases) are first randomly initialized
- For a given layer, initialize weights using Gaussian random variables with μ=0 and σ=1
- Better to use standard deviation 1/√nneurons
- Uniform distribution, and its modifications, also used
Small random subsets, so-called batches, of input–target pairs of the training data set are iteratively used to make small updates on model parameters to minimize the loss function between the predicted values and the observed targets
This minimization is performed by using the gradient of the loss function computed using the backpropagation algorithm
Overflow and underflow
Need to represent infinitely many real numbers with a finite number of fig patterns
The approximation error is always present and can accumulate across many operations
Underflow occurs when numbers near zero are rounded to zero
Overflow occurs when numbers with large magnitude are approximated as ∞ or −∞
Activation function
Activation function takes the sum of weighted inputs as an argument and returns the output of the neuron
a=f(N∑i=0wixi)
where index 0 correspond to the bias term ( x0=b, w0=1 ).
Activation functions
- Adds nonlinearity to the network calculations, allows for flexibility to capture complex nonlinear relationships
- Softmax - applied over a vector z=(z1,...,zK)∈RK of length K as σ(z)i=ezi∑Kj=1ezj
- Sigmoid - f(x)=11+e−x
- Tahn - Hyperbolic tangent tanh(x)=2∗sigmoid(2x)−1
- ReLU - Rectified Linear Unit f(x)=max(x,0).
Other functions: binary step function, linear (i.e., identity) activation function, exponential and scaled exponential linear unit, softplus, softsign
Activation functions overview
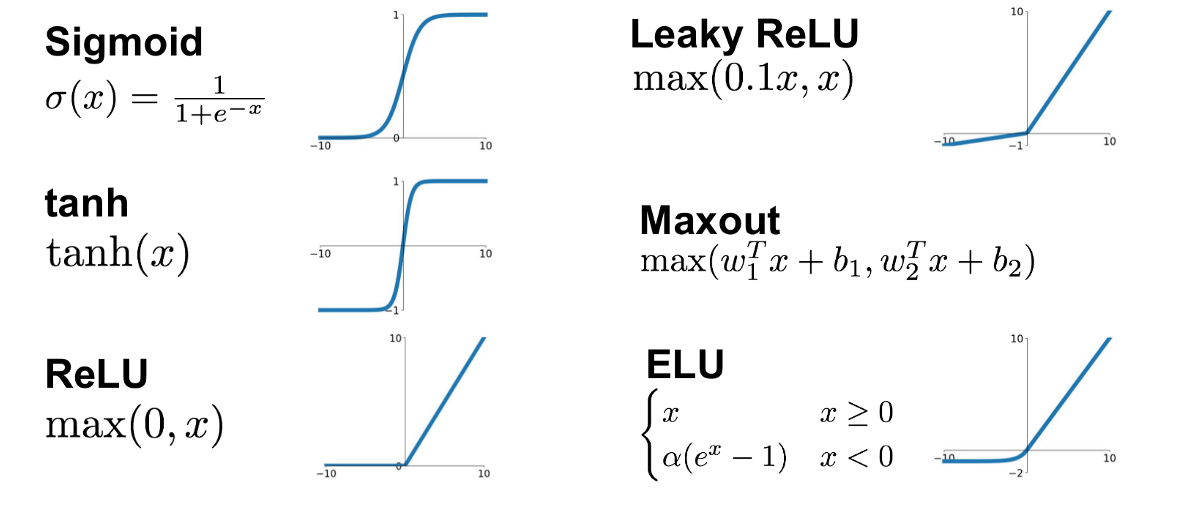
https://towardsdatascience.com/complete-guide-of-activation-functions-34076e95d044
Learning rules
- Optimization - update model parameters on the training data and check its performance on a new validation data to find the most optimal parameters for the best model performance
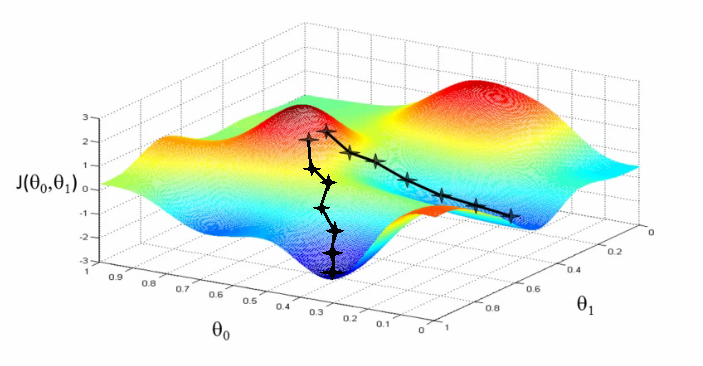
Loss function
- Loss function - (aka objective, or cost function) metric to assess the predictive accuracy, the difference between true and predicted values. Needs to be minimized (or, maximized, metric-dependent)
- Regression loss functions - mean squared error (MSE) MSE=1n∑ni=1(Yi−^Yi)2
- Binary classification loss functions - Binary Cross-Entropy −(ylog(p)+(1−y)log(1−p))
- Multi-class classification loss functions - Multi-class Cross Entropy Loss −∑Mc=1yo,clog(po,c) ( M - number of classes, y - binary indicator if class label c is the correct classification for observation o, p - predicted probability observation o is of class c ), Kullback-Leibler Divergence Loss ∑^y∗log(^yy)
https://ml-cheatsheet.readthedocs.io/en/latest/loss_functions.html
Loss optimization
We want to find the network weights that achieve the lowest loss
W∗=argminW1nn∑i=1L(f(x(i);W),y(i)) where W={W(0),W(1),...}
Gradient descent
An optimization technique - finds a combination of weights for best model performance
Full batch gradient descent uses all the training data to update the weights
Stochastic gradient descent uses parts of the training data
Gradient descent requires calculation of gradient by differentiation of cost function. We can either use first-order differentiation or second-order differentiation
Richards, Blake A., Timothy P. Lillicrap, Philippe Beaudoin, Yoshua Bengio, Rafal Bogacz, Amelia Christensen, Claudia Clopath, et al. “A Deep Learning Framework for Neuroscience.” Nature Neuroscience 2019 - Box 1, Learning and the credit assignment problem
Gradient descent algorithm
Initialize weights randomly ∼N(0,σ2)
Loop until convergence
- Compute gradient, ∂J(W)∂W
- Update weights, W←W−η∂J(W)∂W
Return weights
where η is a learning rate. Right selection is critical - too small may lead to local minima, too large may miss minima entirely. Adaptive implementations exist
Gradient descent algorithms
- Stochastic Gradient Descent (SGD)
- Stochastic Gradient Descent with momentum (Very popular)
- Nesterov's accelerated gradient (NAG)
- Adaptive gradient (AdaGrad)
- Adam (Very good because you need to take less care about learning rate)
- RMSprop
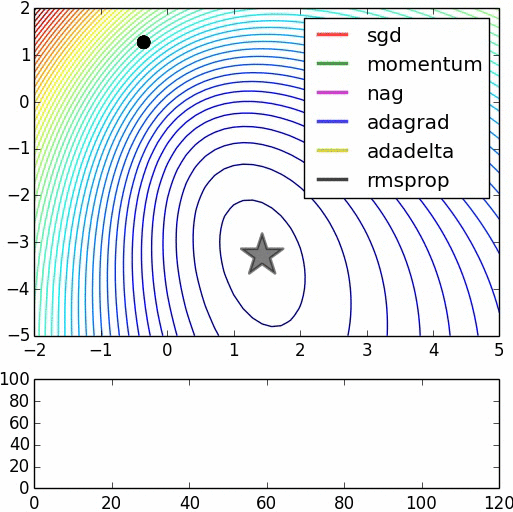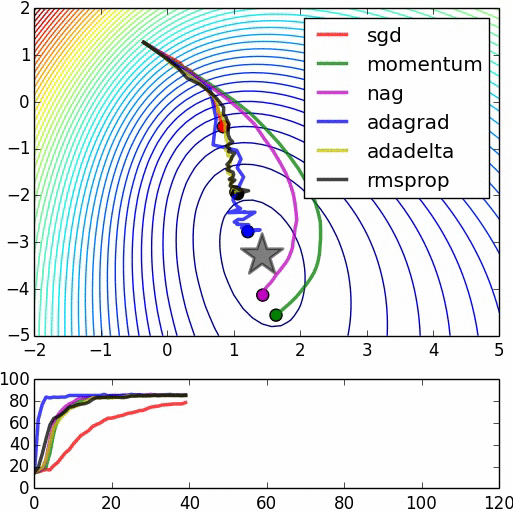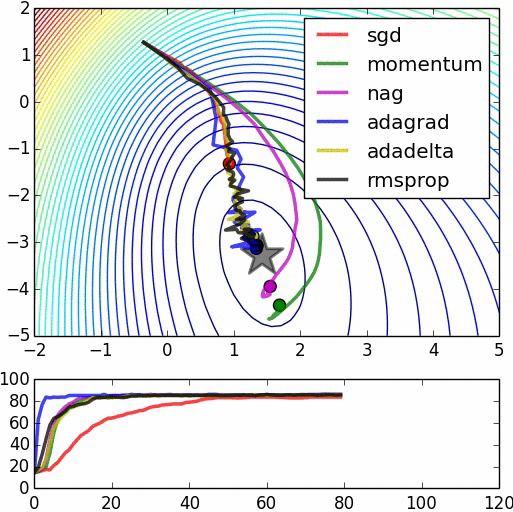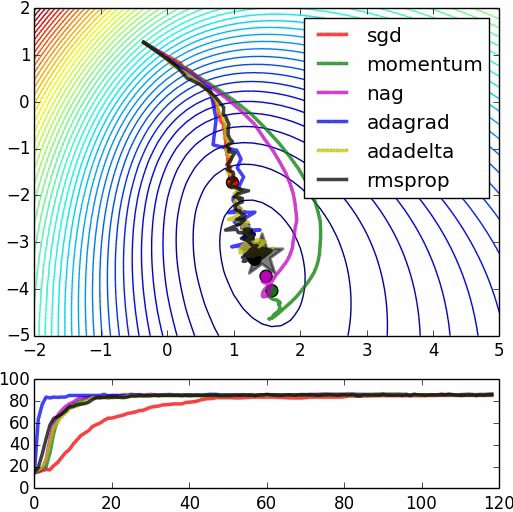
https://leonardoaraujosantos.gitbooks.io/artificial-inteligence/model_optimization.html
Forward and backward propagation
Forward propagation computes the output by passing the input data through the network
The estimated output is compared with the expected output - the error (loss function) is calculated
Backpropagation (the chain rule) propagates the loss back through the network and updates the weights to minimize the loss. Uses chain rule to recursively calculate gradients backward from the output
Each round of forward- and backpropagation is known as one training iteration or epoch
Rumelhart, David E, Geoffrey E Hinton, and Ronald J Williams. “Learning Representations by Back-Propagating Errors,” 1986
Forward propagation
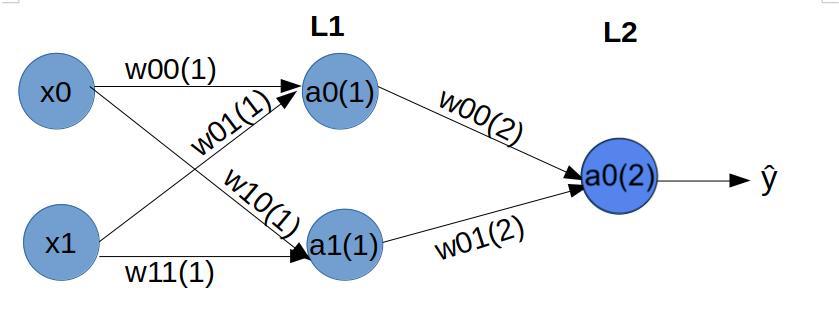
Assuming sigmoid activation function σ(f), at Layer L1, we have:
a10=σ([w100⋅x0+b100]+[w101⋅x1+b101])
a11=σ([w110⋅x0+b110]+[w111⋅x1+b111])
https://www.analyticsvidhya.com/blog/2020/04/comprehensive-popular-deep-learning-interview-questions-answers/
Forward propagation

At Layer L2, we have:
^y=σ([w200⋅a10+b200]+[w201⋅a11+b201])
https://www.analyticsvidhya.com/blog/2020/04/comprehensive-popular-deep-learning-interview-questions-answers/
Backpropagation
Back-propagation - A common method to train neural networks by updating its parameters (i.e., weights) by using the derivative of the network’s performance with respect to the parameters. A technique to calculate gradient through the chain of functions

∂J(W)∂w1=∂J(W)∂^y∗∂^y∂z1∗∂z1∂w1
Review https://ml-cheatsheet.readthedocs.io/en/latest/backpropagation.html
Rumelhart, David E, Geoffrey E Hinton, and Ronald J Williams. “Learning Representations by Back-Propagating Errors”, 1986, 4.
Backpropagation Explained
A series of 10-15 min videos by deeplizard
- Part 1 - The Intuition
- Part 2 - The Mathematical Notation
- Part 3 - Mathematical Observations and the chain rule
- Part 4 - Calculating The Gradient, derivative of the loss function with respect to the weights
- Part 5 - What Puts The "Back" In Backprop?
Analytics Vidhya tutorial: Step-by-step forward and backpropagation, implemented in R and Python: https://www.analyticsvidhya.com/blog/2017/05/neural-network-from-scratch-in-python-and-r/
Vanishing gradient
- Typical deep NNs suffer from the problem of vanishing or exploding gradients
- The gradient descent tries to minimize the error by taking small steps towards the minimum value. These steps are used to update the weights and biases in a neural network
- On the course of backpropagation, the steps may become too small, resulting in negligible updates to weights and bias terms. Thus, a network will be trained with nearly unchanging weights. This is the vanishing gradient problem
- Weights of early layers (latest to be updated) suffer the most
https://en.wikipedia.org/wiki/Vanishing_gradient_problem
Vanishing & Exploding Gradient Explained | A Problem Resulting From Backpropagation
Exploding gradient
- Typical deep NNs suffer from the problem of vanishing or exploding gradients
- The gradient descent tries to minimize the error by taking small steps towards the minimum value. These steps are used to update the weights and biases in a neural network
- The steps may become too large, resulting in large updates to weights and bias terms and potential numerical overflow. This is the exploding gradient problem
- Various solutions exist, typically by propagating a feedback signal from previous layers (residual connections)
https://en.wikipedia.org/wiki/Vanishing_gradient_problem
Vanishing & Exploding Gradient Explained | A Problem Resulting From Backpropagation
The Neural Network Zoo
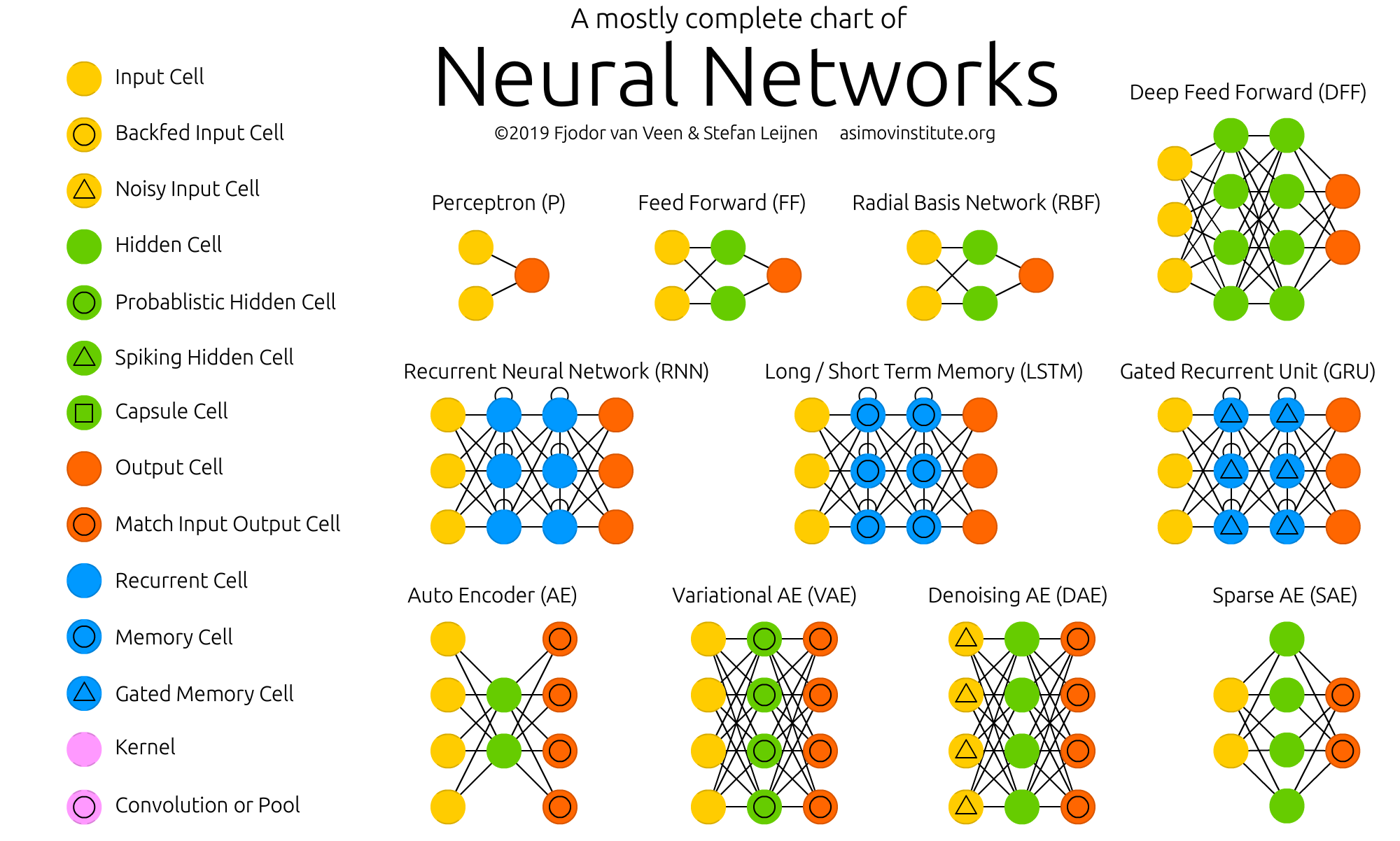
Review the complete infographics at https://www.asimovinstitute.org/neural-network-zoo/